研究課題要旨
本研究の目的は,精度保証付き数値計算や離散可積分系の理論に基づく計算機援用解析手法によって,モデリングの信頼性や現象との整合性について検討できるように理論を展開して,モデリングに役立つ精度保証付き数値計算学を確立し発展させることである.
数理的なモデリングを困難にしている原因として,対象の中に特定できないパラメータや機構が存在する不確定要素問題,入力パラメータの誤差が大きく拡大して結果の予測を困難にしている悪条件性問題,対象の複雑性から莫大な計算による誤差の累積によって結果の精度が著しく損なわれる大規模性問題,モデルの離散化によって構造が変質して,元の問題の性質が変化してしまう構造問題が存在し,実際の現象との整合性が判定不能となることがある.
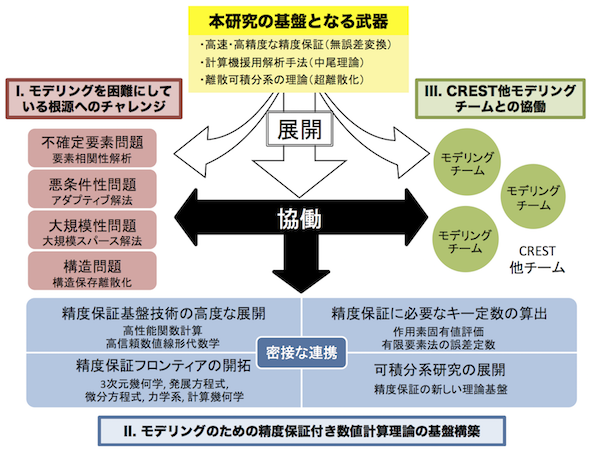
本研究では,以上の諸問題を解決・克服するために,今回の研究参加者が研究・開発してきた本研究課題の基盤理論や基盤技術をベースとし,I.モデリングを困難にしている根源へのチャレンジ,II.モデリングのための精度保証付き数値計算理論の基盤構築,そして,III.他のCRESTモデリングチームとの協働によるモデル方程式に対する信頼性の研究を三本柱として研究展開していく.このような展開を目指すためには,その基礎となる精度保証理論の発展が不可欠となるため,精度保証基盤技術の高度な展開,精度保証に必要な誤差定数(キー定数)の具体的算出,精度保証の新しい理論基盤を構築するために可積分系研究の展開,そして,幅広い観点で数理科学モデリングの信頼性に関連した各種の未解決問題に対する計算機援用解析理論の構築を試みる精度保証理論のフロンティアの開拓を推進する.
研究の目標・ねらい
数理的なモデリング手法が確立していないような新しい分野や,従来の手法ではモデリングが困難な分野におけるモデリング手法の確立に当たって,モデル方程式に対する精度保証付き数値計算や離散可積分系の理論に基づく計算機援用解析手法により,解の存在や(局所)一意性を証明し,解の存在範囲を厳密かつ非常にシャープに特定する手法を開発することによって,モデリングの信頼性や現象との整合性について検討できるように理論を展開して,モデリングに役立つ精度保証付き数値計算学を確立し発展させることを目標とする.
ある現象や分野について,そのモデリング手法を確立するのが難しい場合は,その原因となる困難を乗り越えることが必要である.モデリングを困難にしている原因には次のような問題が考えられる:
(P1)不確定要素問題:モデリング対象の中に,特定できない未知のパラメータや未知の機構が存在する.
(P2)悪条件性問題:モデリング対象が悪条件で,シミュレーションの入力パラメータに混入する誤差が微小であっても,それが大きく拡大して結果の予測を困難にしている.
(P3)大規模性問題:モデリング対象が非常に複雑で,高次元の大規模計算を要求し,計算誤差の累積によって結果の精度が著しく損なわれる.
(P4)構造問題:モデルの離散化によって構造が変質し,元の問題の性質が変化する.
以上のような問題により,定石とされるモデリング手法によって一見正しいモデル方程式を導出したとしても,実際の現象に合致しているのかどうかが判定不能となることがあり得る.
本研究は,以上の諸問題すべてを考慮しながら,モデル方程式の信頼性や現象との整合性の検証などに関わる数学的に厳密かつ高効率な計算機援用解析手法を,精度保証付き数値計算や離散可積分系の理論に基づいて確立し,発展させることをねらいとしている.具体的には,上記に挙げた問題について,数値目標の設定も含めながら,次のように研究展開していく:
(S1)不確定要素問題:不確定要素を精度保証の基本である区間で表現する.区間は実数集合から関数空間まで極めて多様な不確定要素性をモデル化できる.しかしながら,その相互作用を通常の区間演算で表現すると,結果の区間が回転してしまい,いわゆるラッピング・エフェクトによる区間拡大が生じる.これを抑制するために,不確定要素間の相関を考慮に入れて,数万回以上の相互作用であっても高効率に不確定範囲を確定する手法を確立する.
(S2)悪条件性問題:現代の計算機で標準的に利用されている倍精度浮動小数点数は,10進で約16桁の有効数字を持っている.これは,シミュレーションの条件数(入力誤差から出力誤差への拡大率)が10の16乗を越えると,結果の精度は一桁も保証できないことを意味する.これに対して,条件数が10の30乗程度の悪条件問題までは,倍精度計算の数倍程度の手間で高精度な解を高効率に計算する手法を確立する.また,条件数が10の100乗程度までの非常に悪条件な問題についても,適応的かつ高効率に計算できる手法とする.
(S3)大規模性問題:現代のシミュレーションの最前線では,1億次元以上の連立方程式の解を求めるような規模の問題を扱う.この規模になると,良条件問題でも計算誤差が累積して,解の精度が一桁も正しくない現象が多々生じてくる.そこで,高精度計算法を導入し,既存の並列計算法の高速性を保持した1億次元程度の大規模スパース系の高効率な計算法を開発する.
(S4)構造問題:現象をモデリングしてシミュレーションをする場合,基本的には問題を離散方程式に帰着させる.このとき,Lyapunov関数,可積分性,特異性,不安定性,カオス性など,個々の非線形系特有の解構造が挙動に対して支配的であることが多く,汎用の離散化手法ではそれらの構造を壊してしまうことが多い.そこで,共同研究者らが可積分系において発見した差分化・超離散化の手法を展開し,構造保存型の手法およびMax-Plus演算による区間解析の理論を確立し,新しい精度保証手法の開発を行う.また,非線形波動,多粒子系,離散幾何など,従来の精度保証で取り扱わなかった系への応用を目指す.
また,上記のような困難を乗り越えるための展開を目指すに当たり,その基礎となる精度保証理論の発展が不可欠となる.このような基礎面の展開としては,次のような目標を置く.
(S5)精度保証基盤技術の高度な展開:近年の精度保証理論の発展に伴い,特異点を含む関数計算や積分区間・被積分関数が有界でない積分計算などの一般に困難な計算について,多様な分野で高精度かつ高信頼な結果を得ることが求められている.また,連立一次方程式や行列固有値問題などの数値線形代数は,(S2),(S3)の解決に当たり重要な基礎となるため,その高精度かつ高効率な計算アルゴリズムの開発を目指す.これは,従来のような通常の倍精度計算のみでは不可能であり,提案者らの発案した高速精度保証法や無誤差変換法などの計算精度を制御しながら結果精度を保証する高精度計算技術を利用することによって,初めて高速かつ高精度なアルゴリズムの構築が可能になるものである.これらを含め,モデリングの信頼性を与えるための基礎となる高速高精度計算アルゴリズムの開発を行い,本研究の基盤を強化する.
(S6)精度保証に必要なキー定数の具体的算出:数値計算アルゴリズムの収束性を証明するためには,ある定数が存在することが示せれば定性的な評価として十分であったものが,具体的に実際の精度まで把握しながら定量的な評価を与えるためには,できるだけシャープな定数が必要となる.ここでは,数値計算理論に現れる各種の重要なキー定数について,同じ数値計算結果からでも,最終的な誤差評価が大きく改善されるようなシャープな計算法を確立する.
(S7)精度保証フロンティアの開拓:精度保証理論の発展により,様々な問題の計算機援用解析が可能となってきている.そこで,モデル方程式の信頼性を検討する中で,精度保証理論のフロンティアを開拓していく.具体的には,非線形発展方程式,力学系,3次元幾何学問題,計算幾何学など,幅広い観点での数理科学モデリングの信頼性に関連させて,各種の未解決問題に対する計算機援用解析理論の構築を試み,精度保証理論のフロンティアを開拓していく.
(S8)可積分系研究の展開:厳密解や高次保存量を有するような非線形系の理論を基盤として研究を展開する.非線形可積分系の理論は,一般に解の定性的予測すら困難な非線形系の中で,厳密解や保存量に対して明示的な厳密性を持つ系を対象とする理論分野である.本研究では,精度保証と可積分系の共通性に着目し,可積分系理論を基盤として解の保証に対する新しい理論・手法の提案,精度保証が有効となる新しい数理モデルや方程式系の提案を試みる.
以上に加えて,本提案の最も重要なチャレンジとして,CREST他チームの提唱するモデル方程式について,数学的に厳密な信頼性を持った計算機援用解析手法を追求することとしたい.

